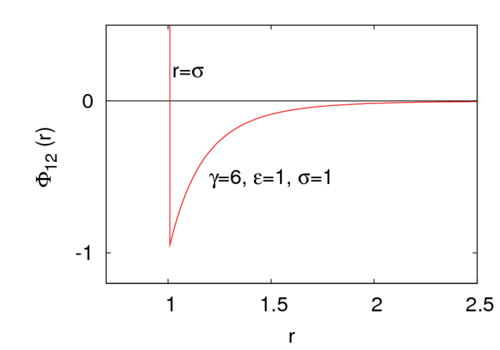Sutherland potential

The Sutherland potential is given by

${\mathrm{\Phi }}_{12}(r)=\{\begin{array}{ccc}\mathrm{\infty }& ;& r\le \sigma \\ -ϵ{(\frac{\sigma }{r})}^{\gamma }& ;& r>\sigma \end{array}$

where ${\mathrm{\Phi }}_{12}(r)$ is the intermolecular pair potential, $r:=|{\mathbf{r}}_1-{\mathbf{r}}_2|$ is the distance between site 1 and site 2, $\sigma$ is the radius of the central hard core, $ϵ$ is the energy well depth ($ϵ>0$), and $\gamma$ is a parameter that controls the interaction range. For example, for $\gamma =6$ the potential look like

References

Related reading

• D. Levi and M. de Llano "Closed form of second virial coefficient for Sutherland potential", Journal of Chemical Physics 63 pp. 4561-4562 (1975)
• Jianxiang Tian and Yuanxing Gui "Liquid-gas phase transition to first order of an argon-like fluid modeled by the hard-core similar Sutherland potential", International Journal of Modern Physics B 18 pp. 2057-2069 (2004)
• A. Díez, J. Largo and J. R. Solana "Structure and thermodynamic properties of Sutherland fluids from computer simulation and the Tang–Lu integral equation theory", Fluid Phase Equilibria 253 pp. 67-73 (2007)
• Jianguo Mi, Yiping Tang, and Chongli Zhong "Theoretical study of Sutherland fluids with long-range, short-range, and highly short-range potential parameters", Journal of Chemical Physics 128 054503 (2008)
• Roman Melnyk, Pedro Orea, Ivo Nezbeda, and Andrij Trokhymchuk "Liquid/vapor coexistence and surface tension of the Sutherland fluid with a variable range of interaction: Computer simulation and perturbation theory studies", Journal of Chemical Physics 132 134504 (2010)
• F. Paragand, F. Feyzi and B. Behzadi "Application of the SAFT-VR equation of state to vapor–liquid equilibrium calculations for pure components and binary mixtures using the Sutherland potential", Fluid Phase Equilibria 290 pp. 181-194 (2010)