Hard superball model

The shape of superballs interpolates between octahedra (q = 0.5) and cubes (q = ∞) via spheres (q = 1).

Phase diagram for hard superballs in the $\phi$ (packing fraction) versus 1/q (bottom axis) and q (top axis) representation where q is the deformation parameter [2].

The hard superball model is defined by the inequality

$|x|^{2q}+|y|^{2q}+|z|^{2q}\leq a^{2q}$

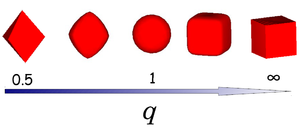
where x, y and z are scaled Cartesian coordinates with q the deformation parameter and radius a. The shape of the superball interpolates smoothly between two Platonic solids, namely the octahedron (q = 0.5) and the cube (q = ∞) via the sphere (q = 1) as shown in the right figure.

Particle Volume

The volume of a superball with the shape parameter q and radius a is given by

Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle {\begin{aligned}v(q,a)&=&8a^{3}\int _{0}^{1}\int _{0}^{(1-x^{2q})^{1/2q}}(1-x^{2q}-y^{2q})^{1/2q}\mathrm {d} \,y\,\mathrm {d} \,x={\frac {2a^{3}\left[\Gamma \left(1/2q\right)\right]^{3}}{3q^{2}\Gamma \left(3/2q\right)}},\end{aligned}}}

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Gamma} is the Gamma function.

Overlap algorithm

The most widely used overlap algorithm is on the basis of Perram and Wertheim method .

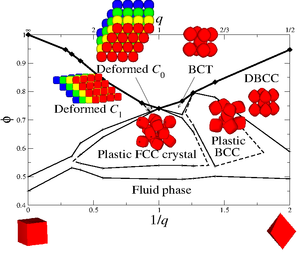
Phase diagram

The full phase diagram of hard superballs whose shape interpolates from cubes to octahedra was reported in Ref .