Hard superball model
A superball is defined by the inequality
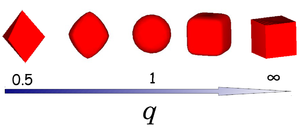
where x, y and z are scaled Cartesian coordinates with q the deformation parameter and radius a. The shape of the superball interpolates smoothly between two Platonic solids, namely the octahedron (q = 0.5) and the cube (q = ∞) via the sphere (q = 1) as shown in the left figure.
Particle Volume
The volume of a superball with the shape parameter "q" and radius "a" is given by
- Failed to parse (unknown function "\begin{eqnarray}"): {\displaystyle \begin{eqnarray} v(q,a) & = & 8 a^3 \int_{0}^1 \int_{0}^{(1-x^{2q})^{1/2q}} (1-x^{2q}-y^{2q})^{1/2q} \mathrm{d}\, y \, \mathrm{d}\, x \nonumber\\ & = & \frac{8a^3\left[ \Gamma\left(1+1/2q\right) \right]^3}{\Gamma\left(1+ 3/2q\right)}, \end{eqnarray} }
