Fused hard sphere chains: Difference between revisions
Jump to navigation
Jump to search
Carl McBride (talk | contribs) No edit summary |
Carl McBride (talk | contribs) No edit summary |
||
| Line 1: | Line 1: | ||
[[Image:FHSC_linear.png|Example of the fused hard sphere chain model, shown here in a linear configuration.|thumb|right]] | [[Image:FHSC_linear.png|Example of the fused hard sphere chain model, shown here in a linear configuration.|thumb|right]] | ||
In the '''fused hard sphere chain''' model the ''molecule'' is built up form a string of overlapping [[hard sphere model|hard sphere sites]], each of diameter <math>\sigma</math>. | |||
An effective number of monomers can be applied to the fused hard sphere chain model by using the relarion (Ref. 4 Eq. 2.18) | |||
<math>m_{\rm effective} = \frac{[1+(m-1)L^*]^3}{[1+(m-1)L^*(3-L^{*2})/2]^2}</math> | |||
where ''m'' is the number of monomer units in the model, and <math>L^*=L/\sigma</math> is the reduced bond length. | |||
The volume of the fused hard sphere chain is given by (Ref. 5 Eq. 13) | |||
:<math>V_{\rm FHSC} =\frac{1}{6} \pi \sigma^3 \left( 1 + \frac{m-1}{2}L^* \left(3-L^{*2}\right) \right)</math> | |||
and the surface area is given by (Ref. 5 Eq. 12) | |||
:<math>S_{\rm FHSC} = \pi \sigma^2 \left( 1+\left( m-1 \right) L^* \right)</math> | |||
==See also== | |||
*[[Rigid fully flexible fused hard sphere model]] | |||
==References== | ==References== | ||
#[http://dx.doi.org/10.1080/00268979100100191 M. Whittle and A. J. Masters "Liquid crystal formation in a system of fused hard spheres", Molecular Physics '''72''' pp. 247-265 (1991)] | #[http://dx.doi.org/10.1080/00268979100100191 M. Whittle and A. J. Masters "Liquid crystal formation in a system of fused hard spheres", Molecular Physics '''72''' pp. 247-265 (1991)] | ||
#[http://dx.doi.org/10.1103/PhysRevE.64.011703 Carl McBride, Carlos Vega, and Luis G. MacDowell "Isotropic-nematic phase transition: Influence of intramolecular flexibility using a fused hard sphere model" Physical Review E '''64''' 011703 (2001)] | #[http://dx.doi.org/10.1103/PhysRevE.64.011703 Carl McBride, Carlos Vega, and Luis G. MacDowell "Isotropic-nematic phase transition: Influence of intramolecular flexibility using a fused hard sphere model" Physical Review E '''64''' 011703 (2001)] | ||
#[http://dx.doi.org/10.1063/1.1517604 Carl McBride and Carlos Vega "A Monte Carlo study of the influence of molecular flexibility on the phase diagram of a fused hard sphere model", Journal of Chemical Physics '''117''' pp. 10370-10379 (2002)] | #[http://dx.doi.org/10.1063/1.1517604 Carl McBride and Carlos Vega "A Monte Carlo study of the influence of molecular flexibility on the phase diagram of a fused hard sphere model", Journal of Chemical Physics '''117''' pp. 10370-10379 (2002)] | ||
#[http://dx.doi.org/10.1063/1.470528 Yaoqi Zhou, Carol K. Hall and George Stell "Thermodynamic perturbation theory for fused hard-sphere and hard-disk chain fluids", Journal of Chemical Physics '''103''' pp. 2688-2695 (1995)] | |||
#[http://dx.doi.org/10.1063/1.459523 T. Boublík, C. Vega, and M. Diaz-Peña "Equation of state of chain molecules", Journal of Chemical Physics '''93''' pp. pp. 730-736 (1990)] | |||
[[category:liquid crystals]] | [[category:liquid crystals]] | ||
[[category:models]] | [[category:models]] | ||
Revision as of 14:58, 18 July 2007
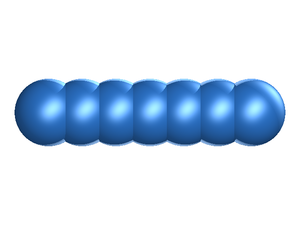
In the fused hard sphere chain model the molecule is built up form a string of overlapping hard sphere sites, each of diameter .
An effective number of monomers can be applied to the fused hard sphere chain model by using the relarion (Ref. 4 Eq. 2.18)
where m is the number of monomer units in the model, and is the reduced bond length.
The volume of the fused hard sphere chain is given by (Ref. 5 Eq. 13)
and the surface area is given by (Ref. 5 Eq. 12)
See also
References
- M. Whittle and A. J. Masters "Liquid crystal formation in a system of fused hard spheres", Molecular Physics 72 pp. 247-265 (1991)
- Carl McBride, Carlos Vega, and Luis G. MacDowell "Isotropic-nematic phase transition: Influence of intramolecular flexibility using a fused hard sphere model" Physical Review E 64 011703 (2001)
- Carl McBride and Carlos Vega "A Monte Carlo study of the influence of molecular flexibility on the phase diagram of a fused hard sphere model", Journal of Chemical Physics 117 pp. 10370-10379 (2002)
- Yaoqi Zhou, Carol K. Hall and George Stell "Thermodynamic perturbation theory for fused hard-sphere and hard-disk chain fluids", Journal of Chemical Physics 103 pp. 2688-2695 (1995)
- T. Boublík, C. Vega, and M. Diaz-Peña "Equation of state of chain molecules", Journal of Chemical Physics 93 pp. pp. 730-736 (1990)

![{\displaystyle m_{\rm {effective}}={\frac {[1+(m-1)L^{*}]^{3}}{[1+(m-1)L^{*}(3-L^{*2})/2]^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/87c971dcd843e41062d341bfbcd501f4edea8001)


