Fused hard sphere chains

Example of the fused hard sphere chain model, shown here in a linear configuration.

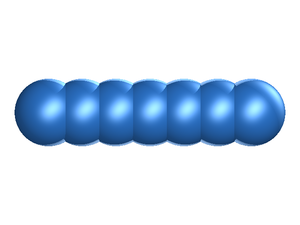
In the fused hard sphere chain model the molecule is built up form a string of overlapping hard sphere sites, each of diameter $\sigma$.

An effective number of monomers can be applied to the fused hard sphere chain model by using the relarion (Ref. 4 Eq. 2.18)

$m_{\rm {effective}}={\frac {[1+(m-1)L^{*}]^{3}}{[1+(m-1)L^{*}(3-L^{*2})/2]^{2}}}$

where m is the number of monomer units in the model, and $L^{*}=L/\sigma$ is the reduced bond length.

The volume of the fused hard sphere chain is given by (Ref. 5 Eq. 13)

$V_{\rm {FHSC}}={\frac {1}{6}}\pi \sigma ^{3}\left(1+(m-1){\frac {L^{*}\left(3-L^{*2}\right)}{2}}\right)$

and the surface area is given by (Ref. 5 Eq. 12)

$S_{\mathrm {F} HSC}=\pi \sigma ^{2}\left(1+\left(m-1\right)L^{*}\right)$

Equation of state

The Vörtler and Nezbeda equation of state is given by

$Z_{\mathrm {FHSC} }=1+(1+3\alpha )\eta _{0}(P^{*})+C_{\rm {FHSC}}[\eta _{0}(P^{*})]^{1.83}$

where

$C_{\rm {FHSC}}=5.66\alpha (1-0.045[\alpha -1]^{1/2}\eta _{0})$

and

$\eta _{0}(P^{*})={\frac {{\sqrt {1+4(1+3\alpha )P^{*}}}-1}{2+6\alpha }}$

1. Horst L. Vörtler and I. Nezbeda "Volume-explicit equation of state and excess volume of mixing of fused hard sphere fluids", Berichte der Bunsen-Gesellschaft 94 pp. 559- (1990)
2. Saidu M. Waziri and Esam Z. Hamad "Volume-Explicit Equation of State for Fused Hard Sphere Chain Fluids", Industrial & Engineering Chemistry Research 47 pp. 9658-9662 (2008)

See also

• Rigid fully flexible fused hard sphere model

References

1. M. Whittle and A. J. Masters "Liquid crystal formation in a system of fused hard spheres", Molecular Physics 72 pp. 247-265 (1991)
2. Carl McBride, Carlos Vega, and Luis G. MacDowell "Isotropic-nematic phase transition: Influence of intramolecular flexibility using a fused hard sphere model" Physical Review E 64 011703 (2001)
3. Carl McBride and Carlos Vega "A Monte Carlo study of the influence of molecular flexibility on the phase diagram of a fused hard sphere model", Journal of Chemical Physics 117 pp. 10370-10379 (2002)
4. Yaoqi Zhou, Carol K. Hall and George Stell "Thermodynamic perturbation theory for fused hard-sphere and hard-disk chain fluids", Journal of Chemical Physics 103 pp. 2688-2695 (1995)
5. T. Boublík, C. Vega, and M. Diaz-Peña "Equation of state of chain molecules", Journal of Chemical Physics 93 pp. pp. 730-736 (1990)
6. Antoine Chamoux and Aurelien Perera "On the linear hard sphere chain fluids", Molecular Physics '93 pp. 649-661 (1998)