Hard sphere model

The hard sphere intermolecular pair potential is defined as

$\Phi _{12}\left(r\right)=\left\{{\begin{array}{lll}\infty &;&r<\sigma \\0&;&r\geq \sigma \end{array}}\right.$

where $\Phi _{12}\left(r\right)$ is the intermolecular pair potential between two spheres at a distance $r$, and $\sigma$ is the diameter of the sphere.

First simulations of hard spheres

The hard sphere model was one of the first ever systems studied:

• Marshall N. Rosenbluth and Arianna W. Rosenbluth "Further Results on Monte Carlo Equations of State", Journal of Chemical Physics 22 pp. 881-884 (1954)
• W. W. Wood and J. D. Jacobson "Preliminary Results from a Recalculation of the Monte Carlo Equation of State of Hard Spheres", Journal of Chemical Physics 27 pp. 1207-1208 (1957)
• B. J. Alder and T. E. Wainwright "Phase Transition for a Hard Sphere System", Journal of Chemical Physics 27 pp. 1208-1209 (1957)

Radial distribution function

The following are a series of plots of the hard sphere radial distribution function (data produced using the computer code written by Jiří Kolafa). Click on image of interest to see a larger view.

$\rho =0.2$ File:HS 0.2 rdf.jpg	$\rho =0.3$ File:HS 0.3 rdf.jpg	$\rho =0.4$ File:HS 0.4 rdf.jpg
$\rho =0.5$ File:HS 0.5 rdf.jpg	$\rho =0.6$ File:HS 0.6 rdf.jpg	$\rho =0.7$ File:HS 0.7 rdf.jpg
$\rho =0.8$ File:HS 0.8 rdf.jpg	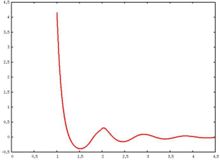$\rho =0.9$	$\rho =1.0$ File:HS 1.0 rdf.jpg

Over the years many groups have studied the radial distribution function of the hard sphere model:

1. John G. Kirkwood, Eugene K. Maun, and Berni J. Alder "Radial Distribution Functions and the Equation of State of a Fluid Composed of Rigid Spherical Molecules", Journal of Chemical Physics 18 pp. 1040- (1950)
2. B. R. A. Nijboer and L. Van Hove "Radial Distribution Function of a Gas of Hard Spheres and the Superposition Approximation", Physical Review 85 pp. 777 - 783 (1952)
3. B. J. Alder, S. P. Frankel, and V. A. Lewinson "Radial Distribution Function Calculated by the Monte-Carlo Method for a Hard Sphere Fluid", Journal of Chemical Physics 23 pp. 417- (1955)
4. Francis H. Ree, R. Norris Keeler, and Shaun L. McCarthy "Radial Distribution Function of Hard Spheres", Journal of Chemical Physics 44 pp. 3407- (1966)
5. W. R. Smith and D. Henderson "Analytical representation of the Percus-Yevick hard-sphere radial distribution function", Molecular Physics 19 pp. 411-415 (1970)
6. J. A. Barker and D. Henderson "Monte Carlo values for the radial distribution function of a system of fluid hard spheres", Molecular Physics 21 pp. 187-191 (1971)
7. J. M. Kincaid and J. J. Weis "Radial distribution function of a hard-sphere solid", Molecular Physics 34 pp. 931-938 (1977)
8. S. Bravo Yuste and A. Santos "Radial distribution function for hard spheres", Physical Review A 43 pp. 5418-5423 (1991)
9. Jaeeon Chang and Stanley I. Sandler "A real function representation for the structure of the hard-sphere fluid", Molecular Physics 81 pp. 735-744 (1994)
10. Andrij Trokhymchuk, Ivo Nezbeda and Jan Jirsák "Hard-sphere radial distribution function again", Journal of Chemical Physics 123 024501 (2005)
11. M. López de Haro, A. Santos and S. B. Yuste "On the radial distribution function of a hard-sphere fluid", Journal of Chemical Physics 124 236102 (2006)

Direct correlation function

For the direct correlation function see:

1. C. F. Tejero and M. López De Haro "Direct correlation function of the hard-sphere fluid", Molecular Physics 105 pp. 2999-3004 (2007)

Fluid-solid transition

The hard sphere system undergoes a fluid-solid first order transition (Ref. 1). The fluid-solid coexistence densities are given by

$\rho _{\mathrm {solid} }^{*}$	$\rho _{\mathrm {liquid} }^{*}$	Reference
1.041	0.945	Ref. 1
1.0376	0.9391	Ref. 2
1.0367(10)	0.9387(10)	Ref. 3
1.0372	0.9387	Ref. 4
1.0369(33)	0.9375(14)	Ref. 5
1.037	0.938	Ref. 6

The coexistence pressure is given by

$p(k_{B}T/\sigma ^{3})$	Reference
11.567	Ref. 2
11.57(10)	Ref. 3
11.54(4)	Ref. 5
11.50(9)	Ref. 7
11.55(11)	Ref. 8

1. William G. Hoover and Francis H. Ree "Melting Transition and Communal Entropy for Hard Spheres", Journal of Chemical Physics 49 pp. 3609-3617 (1968)
2. Daan Frenkel and Berend Smit "Understanding Molecular Simulation: From Algorithms to Applications", Second Edition (2002) (ISBN 0-12-267351-4) p. 261.
3. Andrea Fortini and Marjolein Dijkstra "Phase behaviour of hard spheres confined between parallel hard plates: manipulation of colloidal crystal structures by confinement", Journal of Physics: Condensed Matter 18 pp. L371-L378 (2006)
4. Carlos Vega and Eva G. Noya "Revisiting the Frenkel-Ladd method to compute the free energy of solids: The Einstein molecule approach", Journal of Chemical Physics 127 154113 (2007)
5. Eva G. Noya, Carlos Vega, and Enrique de Miguel "Determination of the melting point of hard spheres from direct coexistence simulation methods", Journal of Chemical Physics 128 154507 (2008)
6. Ruslan L. Davidchack and Brian B. Laird "Simulation of the hard-sphere crystal–melt interface", Journal of Chemical Physics 108 pp. 9452-9462 (1998)
7. N. B. Wilding and A. D. Bruce "Freezing by Monte Carlo Phase Switch", Physical Review Letters 85 pp. 5138-5141 (2000)
8. Robin J. Speedy "Pressure of the metastable hard-sphere fluid", Journal of Physics: Condensed Matter 9 pp. 8591-8599 (1997)

Solid structure

• Leslie V. Woodcock "Computation of the free energy for alternative crystal structures of hard spheres", Faraday Discussions 106 pp. 325 - 338 (1997)

Equations of state

Main article: Equations of state for hard spheres

Virial coefficients

Main article: Hard sphere: virial coefficients

Experimental results

Pusey and van Megen used a suspension of PMMA particles of radius 305 $\pm$10 nm, suspended in poly-12-hydroxystearic acid:

• P. N. Pusey and W. van Megen "Phase behaviour of concentrated suspensions of nearly hard colloidal spheres", Nature 320 pp. 340 - 342 (1986)

For results obtained from the Colloidal Disorder - Order Transition (CDOT) experiments performed on-board the Space Shuttles Columbia and Discovery see Ref. 3.

External links

• Hard disks and spheres computer code on SMAC-wiki.

Related systems

• Polydisperse hard spheres
• Quantum hard spheres
• Dipolar hard spheres

Hard spheres in other dimensions

• 1-dimensional case: hard rods.
• 2-dimensional case: hard disks.
• Hard hyperspheres

References

1. Robin J. Speedy "Pressure of the metastable hard-sphere fluid", Journal of Physics: Condensed Matter 9 pp. 8591-8599 (1997)
2. Robin J. Speedy "Pressure and entropy of hard-sphere crystals", Journal of Physics: Condensed Matter 10 pp. 4387-4391 (1998)
3. Z. Chenga, P. M. Chaikina, W. B. Russelb, W. V. Meyerc, J. Zhub, R. B. Rogersc and R. H. Ottewilld, "Phase diagram of hard spheres", Materials & Design 22 pp. 529-534 (2001)
4. W. R. Smith, D. J. Henderson, P. J. Leonard, J. A. Barker and E. W. Grundke "Fortran codes for the correlation functions of hard sphere fluids", Molecular Physics 106 pp. 3-7 (2008)