Lennard-Jones model

The Lennard-Jones intermolecular pair potential was developed by Sir John Edward Lennard-Jones in 1931 (Ref. 1).

Functional form

The Lennard-Jones potential is given by:

$\Phi (r)=4\epsilon \left[\left({\frac {\sigma }{r}}\right)^{12}-\left({\frac {\sigma }{r}}\right)^{6}\right]$

where:

• $\Phi (r)$ is the intermolecular pair potential between two particles at a distance r;

• $\sigma$ : diameter (length);

• $\epsilon$ : well depth (energy)

Reduced units:

• Density, $\rho ^{*}\equiv \rho \sigma ^{3}$, where $\rho =N/V$ (number of particles $N$ divided by the volume $V$.)

• Temperature; $T^{*}\equiv k_{B}T/\epsilon$, where $T$ is the absolute temperature and $k_{B}$ is the Boltzmann constant

Argon

The Lennard-Jones parameters for argon are $\epsilon /k_{B}\approx$ 119.8 K and $\sigma \approx$ 0.3405 nm. (Ref. ?)

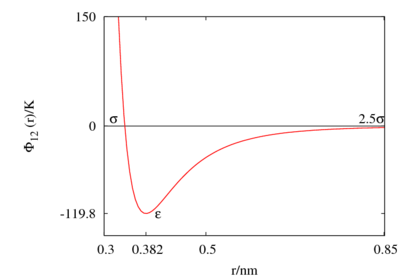
This figure was produced using gnuplot with the command:

plot (4*120*((0.34/x)**12-(0.34/x)**6))

Features

Special points:

• $\Phi (\sigma )=0$
• Minimum value of $\Phi (r)$ at $r=r_{min}$;

${\frac {r_{min}}{\sigma }}=2^{1/6}\simeq 1.12246...$

Critical point

The location of the critical point is (Caillol (Ref. 3))

$T_{c}^{*}=1.326\pm 0.002$

at a reduced density of

$\rho _{c}^{*}=0.316\pm 0.002$.

Triple point

The location of the triple point as found by Mastny and de Pablo (Ref. 2) is

$T_{tp}^{*}=0.694$

Approximations in simulation: truncation and shifting

The Lennard-Jones model is often used with a cutoff radius of $2.5\sigma$. See Mastny and de Pablo (Ref. 2) for an analysis of the effect of this cutoff on the melting line.

m-n Lennard-Jones potential

It is relatively common to encounter potential functions given by:

$\Phi (r)=c_{m,n}\epsilon \left[\left({\frac {\sigma }{r}}\right)^{m}-\left({\frac {\sigma }{r}}\right)^{n}\right].$

with $m$ and $n$ being positive integers and $m>n$. $c_{m,n}$ is chosen such that the minimum value of $\Phi (r)$ being $\Phi _{min}=-\epsilon$. Such forms are usually referred to as m-n Lennard-Jones Potential. For example, the 9-3 Lennard-Jones interaction potential is often used to model the interaction between the atoms/molecules of a fluid and a continuous solid wall. On the '9-3 Lennard-Jones potential' page a justification of this use is presented.

Related pages

• Phase diagram of the Lennard-Jones model
• Lennard-Jones model: virial coefficients
• Lennard-Jones equation of state
• Lennard-Jones sticks
• Lennard-Jones disks
• 9-3 Lennard-Jones potential

References

1. J. E. Lennard-Jones, "Cohesion", Proceedings of the Physical Society, 43 pp. 461-482 (1931)
2. Ethan A. Mastny and Juan J. de Pablo "Melting line of the Lennard-Jones system, infinite size, and full potential", Journal of Chemical Physics 127 104504 (2007)
3. J. M. Caillol " Critical-point of the Lennard-Jones fluid: A finite-size scaling study", Journal of Chemical Physics 109 pp. 4885-4893 (1998)