Lennard-Jones model: Difference between revisions
m (→Features) |
|||
| Line 42: | Line 42: | ||
It is relatively common the use of potential functions given by: | It is relatively common the use of potential functions given by: | ||
: <math> | : <math> \Phi (r) = c_{m,n} \epsilon \left[ \left( \frac{ \sigma }{r } \right)^m - \left( \frac{\sigma}{r} \right)^n | ||
\right]. | \right]. | ||
</math> | </math> | ||
with <math> m </math> and <math> n </math> being positive integer numbers and <math> m > n </math>, and | with <math> m </math> and <math> n </math> being positive integer numbers and <math> m > n </math>, and | ||
<math> c_{m,n} </math> is chosen to get the | <math> c_{m,n} </math> is chosen to get the minimum value of <math> \Phi(r) </math> being <math> \Phi_{min} = - \epsilon </math> | ||
These forms are usually | These forms are usually referred to as '''m-n Lennard-Jones Potential'''. | ||
The 9-3 Lennard-Jones interaction potential is often use to model the interaction between | The 9-3 Lennard-Jones interaction potential is often use to model the interaction between | ||
Revision as of 14:02, 21 June 2007
Lennard-Jones potential
The Lennard-Jones potential, developed by Sir John Edward Lennard-Jones, is given by
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi(r) = 4 \epsilon \left[ \left(\frac{\sigma}{r} \right)^{12}- \left( \frac{\sigma}{r}\right)^6 \right] }
where:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi(r) } is the intermolecular pair potential between two particles at a distance r;
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma } : diameter (length);
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon } : well depth (energy)
Reduced units:
- Density, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho^* \equiv \rho \sigma^3 } , where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho = N/V } (number of particles Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N } divided by the volume Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V } .)
- Temperature; Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T^* \equiv k_B T/\epsilon } , where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T } is the absolute temperature and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_B } is the Boltzmann constant
Argon
The Lennard-Jones parameters for argon are Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon/k_B \approx} 119.8 K and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma \approx} 0.3405 nm. (Ref. ?)
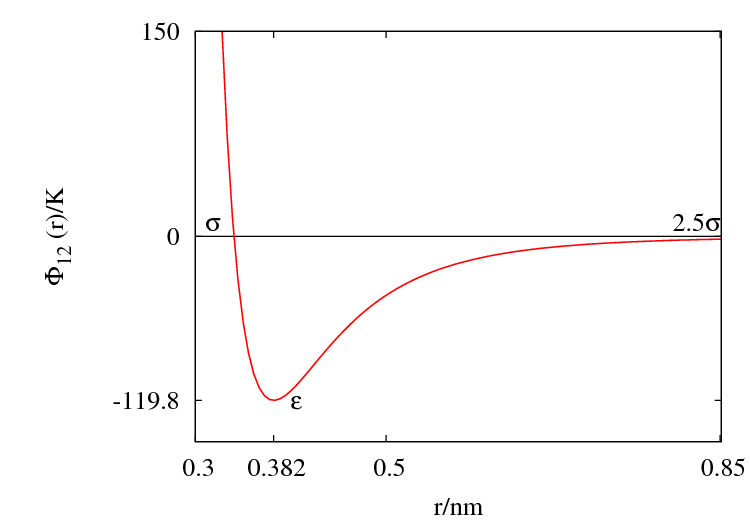
This figure was produced using gnuplot with the command:
plot (4*120*((0.34/x)**12-(0.34/x)**6))
Features
Special points:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi(\sigma) = 0 }
- Minimum value of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi(r) } at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r = r_{min} } ;
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{r_{min}}{\sigma} = 2^{1/6} \simeq 1.12246 ... }
Approximations in simulation: truncation and shifting
Related potential models
It is relatively common the use of potential functions given by:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi (r) = c_{m,n} \epsilon \left[ \left( \frac{ \sigma }{r } \right)^m - \left( \frac{\sigma}{r} \right)^n \right]. }
with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m } and being positive integer numbers and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m > n } , and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c_{m,n} } is chosen to get the minimum value of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi(r) } being Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi_{min} = - \epsilon }
These forms are usually referred to as m-n Lennard-Jones Potential.
The 9-3 Lennard-Jones interaction potential is often use to model the interaction between the atoms/molecules of a fluid and a continuous solid wall. In (9-3 Lennard-Jones potential) a justification of this use is presented.
Other dimensions
- 1-dimensional case: Lennard-Jones rods.
- 2-dimensional case: Lennard-Jones disks.