Path integral formulation: Difference between revisions
Carl McBride (talk | contribs) (Cite tidy.) |
|||
| (20 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
The ''' | The '''path integral formulation''', here from the [[statistical mechanics | statistical mechanical]] point of view, is an elegant method by which [[quantum mechanics | quantum mechanical]] contributions can be incorporated | ||
within a classical simulation using Feynman path integrals (see the [[Path integral formulation#Additional reading|additional reading ]] section). Such simulations are particularly applicable to light atoms and molecules such as [[hydrogen]], [[helium]], [[neon]] and [[argon]], as well as quantum rotators such as [[methane]] and [[water]]. From a more idealised point of view path integrals are often used to study [[quantum hard spheres]]. | within a classical [[Computer simulation techniques |simulation]] using Feynman path integrals (see the [[Path integral formulation#Additional reading|additional reading ]] section). Such simulations are particularly applicable to light atoms and molecules such as [[hydrogen]], [[helium]], [[neon]] and [[argon]], as well as quantum rotators such as [[methane]] and hydrogen-bonded systems such as [[water]]. From a more idealised point of view path integrals are often used to study [[quantum hard spheres]]. | ||
==Principles== | ==Principles== | ||
In the path integral formulation the canonical [[partition function]] (in one dimension) is written as | In the path integral formulation the canonical [[partition function]] (in one dimension) is written as | ||
(<ref name="Berne">[http://dx.doi.org/10.1146/annurev.pc.37.100186.002153 B. J. Berne and D. Thirumalai "On the Simulation of Quantum Systems: Path Integral Methods", Annual Review of Physical Chemistry '''37''' pp. 401-424 (1986)]</ref> Eq. 1) | (<ref name="Berne">[http://dx.doi.org/10.1146/annurev.pc.37.100186.002153 B. J. Berne and D. Thirumalai "On the Simulation of Quantum Systems: Path Integral Methods", Annual Review of Physical Chemistry '''37''' pp. 401-424 (1986)]</ref> Eq. 1) | ||
:<math>Q(\beta, V)= \int {\mathrm d} x_1 \int_{x_1}^{x_1} Dx(\tau)e^{-S[x(\tau)]}</math> | :<math>Q(\beta, V)= \int {\mathrm d} x_1 \int_{x_1}^{x_1} Dx(\tau)e^{-S[x(\tau)]}</math> | ||
where <math>S[x(\tau)]</math> is the | where <math>S[x(\tau)]</math> is the Euclidean action, given by (<ref name="Berne"></ref> Eq. 2) | ||
:<math>S[x(\tau)] = \int_0^{\beta \hbar} H(x(\tau))</math> | :<math>S[x(\tau)] = \int_0^{\beta \hbar} H(x(\tau)) ~{\mathrm d}\tau</math> | ||
where <math>x(\tau)</math> is the path in time <math>\tau</math> and <math>H</math> is the [[Hamiltonian]]. | where <math>x(\tau)</math> is the path in time <math>\tau</math> and <math>H</math> is the [[Hamiltonian]]. | ||
This leads to (<ref name="Berne"> </ref> Eq. 3) | This leads to (<ref name="Berne"></ref> Eq. 3) | ||
:<math>Q_P = \left( \frac{mP}{2 \pi \beta \hbar^2} \right)^{P/2} \int ... \int {\mathrm d}x_1... {\mathrm d}x_P e^{-\beta \Phi_P (x_1...x_P;\beta)}</math> | :<math>Q_P = \left( \frac{mP}{2 \pi \beta \hbar^2} \right)^{P/2} \int ... \int {\mathrm d}x_1... {\mathrm d}x_P e^{-\beta \Phi_P (x_1...x_P;\beta)}</math> | ||
where the Euclidean time is discretised in units of | where the Euclidean time is discretised in units of | ||
| Line 14: | Line 14: | ||
:<math>x_t = x(t \beta \hbar/P)</math> | :<math>x_t = x(t \beta \hbar/P)</math> | ||
:<math>x_{P+1}=x_1</math> | :<math>x_{P+1}=x_1</math> | ||
and (<ref name="Berne"> </ref> Eq. 4) | and (<ref name="Berne"></ref> Eq. 4) | ||
:<math>\Phi_P (x_1...x_P;\beta)= \frac{mP}{2\beta^2 \hbar^2} \sum_{t=1}^P (x_t - x_{t+1})^2 + \frac{1}{P} \sum_{t=1}^P V(x_t)</math> | :<math>\Phi_P (x_1...x_P;\beta)= \frac{mP}{2\beta^2 \hbar^2} \sum_{t=1}^P (x_t - x_{t+1})^2 + \frac{1}{P} \sum_{t=1}^P V(x_t)</math> | ||
where <math>P</math> is the Trotter number. In the Trotter limit, where <math>P \rightarrow \infty</math> these equations become exact. In the case where <math>P=1</math> these equations revert to a classical simulation. It has long been recognised that there is an isomorphism between this discretised quantum mechanical description, and the classical [[statistical mechanics]] of polyatomic fluids, in particular flexible ring molecules<ref>[http://dx.doi.org/10.1063/1.441588 David Chandler and Peter G. Wolynes "Exploiting the isomorphism between quantum theory and classical statistical mechanics of polyatomic fluids", Journal of Chemical Physics '''74''' pp. 4078-4095 (1981)]</ref>, due to the periodic boundary conditions in imaginary time. It can be seen from the first term of the above equation that each particle <math>x_t</math> interacts with is neighbours <math>x_{t-1}</math> and <math>x_{t+1}</math> via a harmonic spring. The second term provides the internal potential energy. | where <math>P</math> is the Trotter number. In the Trotter limit, where <math>P \rightarrow \infty</math> these equations become exact. In the case where <math>P=1</math> these equations revert to a classical simulation. It has long been recognised that there is an isomorphism between this discretised quantum mechanical description, and the classical [[statistical mechanics]] of polyatomic fluids, in particular flexible ring molecules<ref>[http://dx.doi.org/10.1063/1.441588 David Chandler and Peter G. Wolynes "Exploiting the isomorphism between quantum theory and classical statistical mechanics of polyatomic fluids", Journal of Chemical Physics '''74''' pp. 4078-4095 (1981)]</ref>, due to the periodic boundary conditions in imaginary time. It can be seen from the first term of the above equation that each particle <math>x_t</math> interacts with is neighbours <math>x_{t-1}</math> and <math>x_{t+1}</math> via a harmonic spring. The second term provides the internal potential energy. | ||
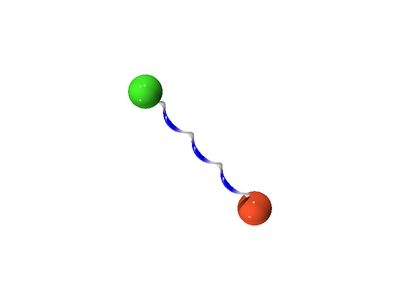
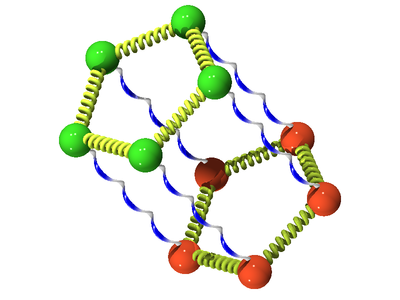
The following is a schematic for the interaction between atom <math>i</math> (green) and atom <math>j</math> (orange). Here we show the atoms having five Trotter slices (<math>P=5</math>), forming what can be thought of as a "ring polymer molecule". The harmonic springs between Trotter slices are in yellow, and white/blue bonds represent the classical [[intermolecular pair potential]]. | |||
:{| border="1" | |||
| [[Image:1bead_classical_ij.png|center|400px]]Classical limit (P=1) || [[Image:5bead_pathIntegra_ij.png|center|400px]] Path integral (here with P=5) | |||
|} | |||
In three dimensions one has the ''density operator'' | |||
:<math>\hat{\rho} (\beta) = \exp\left[ -\beta \hat{H} \right]</math> | :<math>\hat{\rho} (\beta) = \exp\left[ -\beta \hat{H} \right]</math> | ||
| Line 36: | Line 44: | ||
:<math>\langle K_P \rangle = \frac{3NP}{2\beta}- \langle U_{\mathrm {spring}} \rangle </math> | :<math>\langle K_P \rangle = \frac{3NP}{2\beta}- \langle U_{\mathrm {spring}} \rangle </math> | ||
==Harmonic oscillator== | ==Harmonic oscillator== | ||
The density matrix for a harmonic oscillator is given by (<ref>R. P. Feynman and A. R. Hibbs "Path-integrals and Quantum Mechanics", McGraw-Hill, New York (1965) ISBN 0-07-020650-3</ref> Eq. 10-44) | The density matrix for a harmonic oscillator is given by (<ref>R. P. Feynman and A. R. Hibbs "Path-integrals and Quantum Mechanics", McGraw-Hill, New York (1965) ISBN 0-07-020650-3</ref> Eq. 10-44) | ||
| Line 41: | Line 50: | ||
:<math>\rho(x',x)= \sqrt{ \frac{m \omega}{2 \pi \hbar \sinh \omega \beta \hbar} } \exp \left( - \frac{m \omega}{2 \hbar (\sinh \omega \beta \hbar)^2 } \left( (x^2 + x'^2 ) \cosh \omega \beta \hbar - 2xx'\right)\right)</math> | :<math>\rho(x',x)= \sqrt{ \frac{m \omega}{2 \pi \hbar \sinh \omega \beta \hbar} } \exp \left( - \frac{m \omega}{2 \hbar (\sinh \omega \beta \hbar)^2 } \left( (x^2 + x'^2 ) \cosh \omega \beta \hbar - 2xx'\right)\right)</math> | ||
See also refs | |||
<ref>[http://dx.doi.org/10.1119/1.18910 Barry R. Holstein "The harmonic oscillator propagator", American Journal of Physics '''66''' pp. 583-589 (1998)]</ref> | |||
<ref>[http://dx.doi.org/10.1119/1.1715108 L. Moriconi "An elementary derivation of the harmonic oscillator propagator", American Journal of Physics '''72''' pp. 1258-1259 (2004)]</ref> | |||
==Wick rotation and imaginary time== | ==Wick rotation and imaginary time== | ||
One can identify the [[Temperature#Inverse_temperature | inverse temperature]], <math>\beta</math> with an imaginary time <math>it/\hbar</math> (see <ref>M. J. Gillan "The path-integral simulation of quantum systems" in "Computer Modelling of Fluids Polymers and Solids" eds. C. R. A. Catlow, S. C. Parker and M. P. Allen, NATO ASI Series C '''293''' pp. 155-188 (1990) ISBN 978-0-7923-0549-1</ref> § 2.4). | Wick rotation <ref>[http://dx.doi.org/10.1103/PhysRev.96.1124 G. C. Wick "Properties of Bethe-Salpeter Wave Functions", Physical Review '''96''' pp. 1124-1134 (1954)]</ref>. One can identify the [[Temperature#Inverse_temperature | inverse temperature]], <math>\beta</math> with an imaginary time <math>it/\hbar</math> (see <ref>M. J. Gillan "The path-integral simulation of quantum systems" in "Computer Modelling of Fluids Polymers and Solids" eds. C. R. A. Catlow, S. C. Parker and M. P. Allen, NATO ASI Series C '''293''' pp. 155-188 (1990) ISBN 978-0-7923-0549-1</ref> § 2.4). | ||
==Rotational degrees of freedom== | ==Rotational degrees of freedom== | ||
In the case of systems having (<math>d</math>) rotational [[degree of freedom | degrees of freedom]] the [[Hamiltonian]] can be written in the form (<ref name="Marx">[http://dx.doi.org/10.1088/0953-8984/11/11/003 Dominik Marx and Martin H Müser "Path integral simulations of rotors: theory and applications", Journal of Physics: Condensed Matter '''11''' pp. R117-R155 (1999)]</ref> Eq. 2.1): | In the case of systems having (<math>d</math>) rotational [[degree of freedom | degrees of freedom]] the [[Hamiltonian]] can be written in the form (<ref name="Marx">[http://dx.doi.org/10.1088/0953-8984/11/11/003 Dominik Marx and Martin H Müser "Path integral simulations of rotors: theory and applications", Journal of Physics: Condensed Matter '''11''' pp. R117-R155 (1999)]</ref> Eq. 2.1): | ||
:<math>\hat{H} = \hat{T}^{\mathrm {translational}} + \hat{T}^{\mathrm {rotational}}+ \hat{V}</math> | :<math>\hat{H} = \hat{T}^{\mathrm {translational}} + \hat{T}^{\mathrm {rotational}}+ \hat{V}</math> | ||
where the rotational part of the kinetic energy operator is given by (<ref name="Marx"> </ref> Eq. 2.2) | where the rotational part of the kinetic energy operator is given by (<ref name="Marx"></ref> Eq. 2.2) | ||
:<math>T^{\mathrm {rotational}} = \sum_{i=1}^{d^{\mathrm {rotational}}} \frac{\hat{L}_i^2}{2\Theta_{ii}}</math> | :<math>T^{\mathrm {rotational}} = \sum_{i=1}^{d^{\mathrm {rotational}}} \frac{\hat{L}_i^2}{2\Theta_{ii}}</math> | ||
where <math>\hat{L}_i</math> are the components of the angular momentum operator, and <math>\Theta_{ii}</math> are the moments of inertia. | where <math>\hat{L}_i</math> are the components of the angular momentum operator, and <math>\Theta_{ii}</math> are the moments of inertia. | ||
==Rigid rotators== | |||
:''Main article: [[Rigid top propagator]]'' | |||
==Computer simulation techniques== | |||
The following are a number of commonly used [[computer simulation techniques]] that make use of the path integral formulation applied to phases of condensed matter | |||
====Path integral Monte Carlo==== | ====Path integral Monte Carlo==== | ||
Path integral Monte Carlo (PIMC) | Path integral Monte Carlo (PIMC) | ||
<ref>[http://dx.doi.org/10.1063/1.437829 J. A. Barker "A quantum-statistical Monte Carlo method; path integrals with boundary conditions", Journal of Chemical Physics '''70''' pp. 2914- (1979)]</ref> | |||
====Path integral molecular dynamics==== | ====Path integral molecular dynamics==== | ||
Path integral molecular dynamics (PIMD) | Path integral molecular dynamics (PIMD) | ||
<ref>[http://dx.doi.org/10.1063/1.446740 M. Parrinello and A. Rahman "Study of an F center in molten KCl", Journal of Chemical Physics '''80''' pp. 860- (1984)]</ref> | |||
====Centroid molecular dynamics==== | ====Centroid molecular dynamics==== | ||
Centroid molecular dynamics (CMD) | Centroid molecular dynamics (CMD) | ||
<ref>[http://dx.doi.org/10.1063/1.467175 Jianshu Cao and Gregory A. Voth "The formulation of quantum statistical mechanics based on the Feynman path centroid density. I. Equilibrium properties", Journal of Chemical Physics '''100''' pp. 5093-5105 (1994)]</ref> | |||
<ref>[http://dx.doi.org/10.1063/1.467176 Jianshu Cao and Gregory A. Voth "The formulation of quantum statistical mechanics based on the Feynman path centroid density. II. Dynamical properties", Journal of Chemical Physics '''100''' pp. 5106- (1994)]</ref> | |||
<ref>[http://dx.doi.org/10.1063/1.479515 Seogjoo Jang and Gregory A. Voth "A derivation of centroid molecular dynamics and other approximate time evolution methods for path integral centroid variables", Journal of Chemical Physics '''111''' pp. 2371- (1999)]</ref> | |||
<ref>[http://dx.doi.org/10.1063/1.479666 Rafael Ramírez and Telesforo López-Ciudad "The Schrödinger formulation of the Feynman path centroid density", Journal of Chemical Physics '''111''' pp. 3339-3348 (1999)]</ref> | |||
<ref>[http://dx.doi.org/10.1063/1.3484490 E. A. Polyakov, A. P. Lyubartsev, and P. N. Vorontsov-Velyaminov "Centroid molecular dynamics: Comparison with exact results for model systems", Journal of Chemical Physics '''133''' 194103 (2010)]</ref> | |||
====Ring polymer molecular dynamics==== | ====Ring polymer molecular dynamics==== | ||
Ring polymer molecular dynamics (RPMD) | Ring polymer molecular dynamics (RPMD) | ||
<ref>[http://dx.doi.org/10.1063/1.1777575 Ian R. Craig and David E. Manolopoulos "Quantum statistics and classical mechanics: Real time correlation functions from ring polymer molecular dynamics", Journal of Chemical Physics '''121''' pp. 3368- (2004)]</ref> | |||
<ref>[http://dx.doi.org/10.1063/1.2357599 Bastiaan J. Braams and David E. Manolopoulos "On the short-time limit of ring polymer molecular dynamics", Journal of Chemical Physics '''125''' 124105 (2006)]</ref> | |||
(Contraction scheme | |||
<ref>[http://dx.doi.org/10.1063/1.2953308 Thomas E. Markland and David E. Manolopoulos "An efficient ring polymer contraction scheme for imaginary time path integral simulations", Journal of Chemical Physics '''129''' 024105 (2008)]</ref> | |||
<ref>[http://dx.doi.org/10.1016/j.cplett.2008.09.019 Thomas E. Markland and David E. Manolopoulos "A refined ring polymer contraction scheme for systems with electrostatic interactions" Chemical Physics Letters '''464''' pp. 256-261 (2008)]</ref>) | |||
====Car-Parrinello path-integral molecular dynamics==== | |||
Path-integral [[Car-Parrinello technique]]<ref>[http://dx.doi.org/10.1007/BF01312185 Dominik Marx and Michele Parrinello "Ab initio path-integral molecular dynamics", Zeitschrift für Physik B Condensed Matter '''95''' pp. 143-144 (1994)]</ref> | |||
<ref>[http://dx.doi.org/10.1063/1.471221 Dominik Marx and Michele Parrinello "Ab initio path integral molecular dynamics: Basic ideas", Journal of Chemical Physics '''104''' pp. 4077 (1996)]</ref> | |||
<ref>[http://dx.doi.org/10.1103/PhysRevE.93.043305 Christopher John, Thomas Spura, Scott Habershon, and Thomas D. Kühne "Quantum ring-polymer contraction method: Including nuclear quantum effects at no additional computational cost in comparison to ab initio molecular dynamics", Physical Review E '''93''' pp. 043305 (2016)]</ref> | |||
====Normal mode PIMD==== | ====Normal mode PIMD==== | ||
====Grand canonical Monte Carlo==== | ====Grand canonical Monte Carlo==== | ||
A path integral version of the [[Widom test-particle method]] for [[grand canonical Monte Carlo]] simulations: | A path integral version of the [[Widom test-particle method]] for [[grand canonical Monte Carlo]] simulations: | ||
<ref>[http://dx.doi.org/10.1063/1.474874 Qinyu Wang, J. Karl Johnson and Jeremy Q. Broughton "Path integral grand canonical Monte Carlo", Journal of Chemical Physics '''107''' pp. 5108-5117 (1997)]</ref> | |||
==Applications== | ==Applications== | ||
<ref>[http://dx.doi.org/10.1063/1.470898 Jianshu Cao and Gregory A. Voth "Semiclassical approximations to quantum dynamical time correlation functions", Journal of Chemical Physics '''104''' pp. 273-285 (1996)]</ref> | |||
<ref>[http://dx.doi.org/10.1063/1.1316105 C. Chakravarty and R. M. Lynden-Bell "Landau free energy curves for melting of quantum solids", Journal of Chemical Physics '''113''' pp. 9239-9247 (2000)]</ref> | |||
==References== | ==References== | ||
<references/> | <references/> | ||
==Additional reading== | ==Additional reading== | ||
* P. A. M. Dirac "The Lagrangian in Quantum Mechanics", Physikalische Zeitschrift der Sowjetunion '''3''' pp. 64-72 (1933) | |||
*R. P. Feynman "Statistical Mechanics", Benjamin, Reading, Massachusetts, (1972) ISBN 0-201-36076-4 Chapter 3. | *R. P. Feynman "Statistical Mechanics", Benjamin, Reading, Massachusetts, (1972) ISBN 0-201-36076-4 Chapter 3. | ||
*[http://dx.doi.org/10.1143/JPSJ.35.980 Tohru Morita "Solution of the Bloch Equation for Many-Particle Systems in Terms of the Path Integral", Journal of the Physical Society of Japan '''35''' pp. 980-984 (1973)] | |||
*[http://dx.doi.org/10.1016/0370-1573(75)90030-7 F. W. Wiegel "Path integral methods in statistical mechanics", Physics Reports '''16''' pp. 57-114 (1975)] | |||
*[http://dx.doi.org/10.1063/1.437829 J. A. Barker "A quantum-statistical Monte Carlo method; path integrals with boundary conditions", Journal of Chemical Physics '''70''' pp. 2914-2918 (1979)] | |||
*[http://dx.doi.org/10.1103/RevModPhys.67.279 D. M. Ceperley "Path integrals in the theory of condensed helium", Reviews of Modern Physics '''67''' 279 - 355 (1995)] | *[http://dx.doi.org/10.1103/RevModPhys.67.279 D. M. Ceperley "Path integrals in the theory of condensed helium", Reviews of Modern Physics '''67''' 279 - 355 (1995)] | ||
*[http://dx.doi.org/10.1080/014423597230190 Charusita Chakravarty "Path integral simulations of atomic and molecular systems", International Reviews in Physical Chemistry '''16''' pp. 421-444 (1997)] | *[http://dx.doi.org/10.1080/014423597230190 Charusita Chakravarty "Path integral simulations of atomic and molecular systems", International Reviews in Physical Chemistry '''16''' pp. 421-444 (1997)] | ||
*[http://www.scholarpedia.org/article/Path_integral Jean Zinn-Justin "Path integral" Scholarpedia, 4(2):8674 (2009)] | |||
==External links== | ==External links== | ||
*[http://www.smac.lps.ens.fr/index.php/Programs_Chapter_3:_Density_matrices_and_path_integrals Density matrices and path integrals] computer code on SMAC-wiki. | *[http://www.smac.lps.ens.fr/index.php/Programs_Chapter_3:_Density_matrices_and_path_integrals Density matrices and path integrals] computer code on SMAC-wiki. | ||
*[http://www.deleramentum.net/codes/repimd/ A simple implementation of PIMD integrator (C++).] | |||
[[Category: Monte Carlo]] | [[Category: Monte Carlo]] | ||
[[category: Quantum mechanics]] | [[category: Quantum mechanics]] | ||
Latest revision as of 21:04, 7 September 2020
The path integral formulation, here from the statistical mechanical point of view, is an elegant method by which quantum mechanical contributions can be incorporated within a classical simulation using Feynman path integrals (see the additional reading section). Such simulations are particularly applicable to light atoms and molecules such as hydrogen, helium, neon and argon, as well as quantum rotators such as methane and hydrogen-bonded systems such as water. From a more idealised point of view path integrals are often used to study quantum hard spheres.
Principles[edit]
In the path integral formulation the canonical partition function (in one dimension) is written as ([1] Eq. 1)
where is the Euclidean action, given by ([1] Eq. 2)
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x(\tau)} is the path in time Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H} is the Hamiltonian. This leads to ([1] Eq. 3)
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q_P = \left( \frac{mP}{2 \pi \beta \hbar^2} \right)^{P/2} \int ... \int {\mathrm d}x_1... {\mathrm d}x_P e^{-\beta \Phi_P (x_1...x_P;\beta)}}
where the Euclidean time is discretised in units of
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_t = x(t \beta \hbar/P)}
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_{P+1}=x_1}
and ([1] Eq. 4)
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi_P (x_1...x_P;\beta)= \frac{mP}{2\beta^2 \hbar^2} \sum_{t=1}^P (x_t - x_{t+1})^2 + \frac{1}{P} \sum_{t=1}^P V(x_t)}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P} is the Trotter number. In the Trotter limit, where these equations become exact. In the case where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P=1} these equations revert to a classical simulation. It has long been recognised that there is an isomorphism between this discretised quantum mechanical description, and the classical statistical mechanics of polyatomic fluids, in particular flexible ring molecules[2], due to the periodic boundary conditions in imaginary time. It can be seen from the first term of the above equation that each particle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_t} interacts with is neighbours Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_{t-1}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_{t+1}} via a harmonic spring. The second term provides the internal potential energy.
The following is a schematic for the interaction between atom (green) and atom Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j} (orange). Here we show the atoms having five Trotter slices (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P=5} ), forming what can be thought of as a "ring polymer molecule". The harmonic springs between Trotter slices are in yellow, and white/blue bonds represent the classical intermolecular pair potential.
In three dimensions one has the density operator
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{\rho} (\beta) = \exp\left[ -\beta \hat{H} \right]}
which thanks to the Trotter formula we can tease out Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \exp \left[ -\beta (U_{\mathrm {spring}}+ U_{\mathrm{internal}} ) \right]} , where
and
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U_{\mathrm{internal}}= \frac{1}{P} \sum_{t=1}^P V(\mathbf{r}_t)}
The internal energy is given by
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle U \rangle = \frac{3NP}{2\beta}- \langle U_{\mathrm {spring}} \rangle + \langle U_{\mathrm{internal}} \rangle }
The average kinetic energy is known as the primitive estimator, i.e.
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle K_P \rangle = \frac{3NP}{2\beta}- \langle U_{\mathrm {spring}} \rangle }
Harmonic oscillator[edit]
The density matrix for a harmonic oscillator is given by ([3] Eq. 10-44)
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho(x',x)= \sqrt{ \frac{m \omega}{2 \pi \hbar \sinh \omega \beta \hbar} } \exp \left( - \frac{m \omega}{2 \hbar (\sinh \omega \beta \hbar)^2 } \left( (x^2 + x'^2 ) \cosh \omega \beta \hbar - 2xx'\right)\right)}
Wick rotation and imaginary time[edit]
Wick rotation [6]. One can identify the inverse temperature, with an imaginary time Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle it/\hbar} (see [7] § 2.4).
Rotational degrees of freedom[edit]
In the case of systems having (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d} ) rotational degrees of freedom the Hamiltonian can be written in the form ([8] Eq. 2.1):
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{H} = \hat{T}^{\mathrm {translational}} + \hat{T}^{\mathrm {rotational}}+ \hat{V}}
where the rotational part of the kinetic energy operator is given by ([8] Eq. 2.2)
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T^{\mathrm {rotational}} = \sum_{i=1}^{d^{\mathrm {rotational}}} \frac{\hat{L}_i^2}{2\Theta_{ii}}}
where are the components of the angular momentum operator, and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Theta_{ii}} are the moments of inertia.
Rigid rotators[edit]
- Main article: Rigid top propagator
Computer simulation techniques[edit]
The following are a number of commonly used computer simulation techniques that make use of the path integral formulation applied to phases of condensed matter
Path integral Monte Carlo[edit]
Path integral Monte Carlo (PIMC) [9]
Path integral molecular dynamics[edit]
Path integral molecular dynamics (PIMD) [10]
Centroid molecular dynamics[edit]
Centroid molecular dynamics (CMD) [11] [12] [13] [14] [15]
Ring polymer molecular dynamics[edit]
Ring polymer molecular dynamics (RPMD) [16] [17] (Contraction scheme [18] [19])
Car-Parrinello path-integral molecular dynamics[edit]
Path-integral Car-Parrinello technique[20] [21] [22]
Normal mode PIMD[edit]
Grand canonical Monte Carlo[edit]
A path integral version of the Widom test-particle method for grand canonical Monte Carlo simulations: [23]
Applications[edit]
References[edit]
- ↑ 1.0 1.1 1.2 1.3 B. J. Berne and D. Thirumalai "On the Simulation of Quantum Systems: Path Integral Methods", Annual Review of Physical Chemistry 37 pp. 401-424 (1986)
- ↑ David Chandler and Peter G. Wolynes "Exploiting the isomorphism between quantum theory and classical statistical mechanics of polyatomic fluids", Journal of Chemical Physics 74 pp. 4078-4095 (1981)
- ↑ R. P. Feynman and A. R. Hibbs "Path-integrals and Quantum Mechanics", McGraw-Hill, New York (1965) ISBN 0-07-020650-3
- ↑ Barry R. Holstein "The harmonic oscillator propagator", American Journal of Physics 66 pp. 583-589 (1998)
- ↑ L. Moriconi "An elementary derivation of the harmonic oscillator propagator", American Journal of Physics 72 pp. 1258-1259 (2004)
- ↑ G. C. Wick "Properties of Bethe-Salpeter Wave Functions", Physical Review 96 pp. 1124-1134 (1954)
- ↑ M. J. Gillan "The path-integral simulation of quantum systems" in "Computer Modelling of Fluids Polymers and Solids" eds. C. R. A. Catlow, S. C. Parker and M. P. Allen, NATO ASI Series C 293 pp. 155-188 (1990) ISBN 978-0-7923-0549-1
- ↑ 8.0 8.1 Dominik Marx and Martin H Müser "Path integral simulations of rotors: theory and applications", Journal of Physics: Condensed Matter 11 pp. R117-R155 (1999)
- ↑ J. A. Barker "A quantum-statistical Monte Carlo method; path integrals with boundary conditions", Journal of Chemical Physics 70 pp. 2914- (1979)
- ↑ M. Parrinello and A. Rahman "Study of an F center in molten KCl", Journal of Chemical Physics 80 pp. 860- (1984)
- ↑ Jianshu Cao and Gregory A. Voth "The formulation of quantum statistical mechanics based on the Feynman path centroid density. I. Equilibrium properties", Journal of Chemical Physics 100 pp. 5093-5105 (1994)
- ↑ Jianshu Cao and Gregory A. Voth "The formulation of quantum statistical mechanics based on the Feynman path centroid density. II. Dynamical properties", Journal of Chemical Physics 100 pp. 5106- (1994)
- ↑ Seogjoo Jang and Gregory A. Voth "A derivation of centroid molecular dynamics and other approximate time evolution methods for path integral centroid variables", Journal of Chemical Physics 111 pp. 2371- (1999)
- ↑ Rafael Ramírez and Telesforo López-Ciudad "The Schrödinger formulation of the Feynman path centroid density", Journal of Chemical Physics 111 pp. 3339-3348 (1999)
- ↑ E. A. Polyakov, A. P. Lyubartsev, and P. N. Vorontsov-Velyaminov "Centroid molecular dynamics: Comparison with exact results for model systems", Journal of Chemical Physics 133 194103 (2010)
- ↑ Ian R. Craig and David E. Manolopoulos "Quantum statistics and classical mechanics: Real time correlation functions from ring polymer molecular dynamics", Journal of Chemical Physics 121 pp. 3368- (2004)
- ↑ Bastiaan J. Braams and David E. Manolopoulos "On the short-time limit of ring polymer molecular dynamics", Journal of Chemical Physics 125 124105 (2006)
- ↑ Thomas E. Markland and David E. Manolopoulos "An efficient ring polymer contraction scheme for imaginary time path integral simulations", Journal of Chemical Physics 129 024105 (2008)
- ↑ Thomas E. Markland and David E. Manolopoulos "A refined ring polymer contraction scheme for systems with electrostatic interactions" Chemical Physics Letters 464 pp. 256-261 (2008)
- ↑ Dominik Marx and Michele Parrinello "Ab initio path-integral molecular dynamics", Zeitschrift für Physik B Condensed Matter 95 pp. 143-144 (1994)
- ↑ Dominik Marx and Michele Parrinello "Ab initio path integral molecular dynamics: Basic ideas", Journal of Chemical Physics 104 pp. 4077 (1996)
- ↑ Christopher John, Thomas Spura, Scott Habershon, and Thomas D. Kühne "Quantum ring-polymer contraction method: Including nuclear quantum effects at no additional computational cost in comparison to ab initio molecular dynamics", Physical Review E 93 pp. 043305 (2016)
- ↑ Qinyu Wang, J. Karl Johnson and Jeremy Q. Broughton "Path integral grand canonical Monte Carlo", Journal of Chemical Physics 107 pp. 5108-5117 (1997)
- ↑ Jianshu Cao and Gregory A. Voth "Semiclassical approximations to quantum dynamical time correlation functions", Journal of Chemical Physics 104 pp. 273-285 (1996)
- ↑ C. Chakravarty and R. M. Lynden-Bell "Landau free energy curves for melting of quantum solids", Journal of Chemical Physics 113 pp. 9239-9247 (2000)
Additional reading[edit]
- P. A. M. Dirac "The Lagrangian in Quantum Mechanics", Physikalische Zeitschrift der Sowjetunion 3 pp. 64-72 (1933)
- R. P. Feynman "Statistical Mechanics", Benjamin, Reading, Massachusetts, (1972) ISBN 0-201-36076-4 Chapter 3.
- Tohru Morita "Solution of the Bloch Equation for Many-Particle Systems in Terms of the Path Integral", Journal of the Physical Society of Japan 35 pp. 980-984 (1973)
- F. W. Wiegel "Path integral methods in statistical mechanics", Physics Reports 16 pp. 57-114 (1975)
- J. A. Barker "A quantum-statistical Monte Carlo method; path integrals with boundary conditions", Journal of Chemical Physics 70 pp. 2914-2918 (1979)
- D. M. Ceperley "Path integrals in the theory of condensed helium", Reviews of Modern Physics 67 279 - 355 (1995)
- Charusita Chakravarty "Path integral simulations of atomic and molecular systems", International Reviews in Physical Chemistry 16 pp. 421-444 (1997)
- Jean Zinn-Justin "Path integral" Scholarpedia, 4(2):8674 (2009)
External links[edit]
- Density matrices and path integrals computer code on SMAC-wiki.
- A simple implementation of PIMD integrator (C++).
![{\displaystyle Q(\beta ,V)=\int {\mathrm {d} }x_{1}\int _{x_{1}}^{x_{1}}Dx(\tau )e^{-S[x(\tau )]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5652acf277a02f93012e3fd34ac6cea585b0daee)
![{\displaystyle S[x(\tau )]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8bf07e76471abd2ca6098a657e600dc5a43c742d)
![{\displaystyle S[x(\tau )]=\int _{0}^{\beta \hbar }H(x(\tau ))~{\mathrm {d} }\tau }](https://wikimedia.org/api/rest_v1/media/math/render/svg/bb83863beff9c8a2e09a152047fc3d5063b37306)