Radial distribution function: Difference between revisions
Carl McBride (talk | contribs) No edit summary |
Carl McBride (talk | contribs) m (Updated a reference) |
||
| (13 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
The '''radial distribution function''' is a special case of the [[pair distribution function]] for an isotropic system. | |||
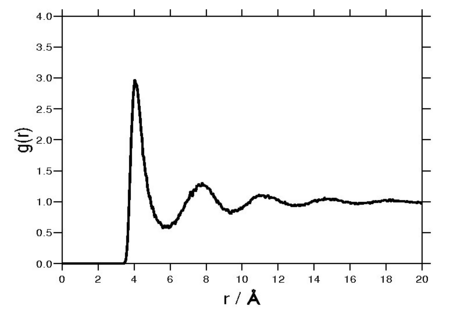
A [[Fourier analysis | Fourier transform]] of the radial distribution function results in the [[structure factor]], which is experimentally measurable. The following plot is of a typical radial distribution function for the monatomic [[Lennard-Jones model |Lennard-Jones]] liquid. | |||
[[Image:LJ_rdf.png|center|450px|Typical radial distribution function for the monatomic Lennard-Jones liquid.]] | |||
==Density Expansion of the radial distribution function== | ==Density Expansion of the radial distribution function== | ||
The '''radial distribution function''' of a compressed gas may be expanded in powers of the density ( | The '''radial distribution function''' of a compressed gas may be expanded in powers of the density <ref>[http://dx.doi.org/10.1103/PhysRev.85.777 B. R. A. Nijboer and L. Van Hove "Radial Distribution Function of a Gas of Hard Spheres and the Superposition Approximation", Physical Review '''85''' pp. 777-783 (1952)]</ref> | ||
:<math>\left. {\rm g}(r) \right. = e^{-\beta \Phi(r)} (1 + \rho {\rm g}_1 (r) + \rho^2 {\rm g}_2 (r) + ...)</math> | :<math>\left. {\rm g}(r) \right. = e^{-\beta \Phi(r)} (1 + \rho {\rm g}_1 (r) + \rho^2 {\rm g}_2 (r) + ...)</math> | ||
| Line 11: | Line 14: | ||
In classical mechanics, and on the assumption of additivity of intermolecular forces, one has | In classical mechanics, and on the assumption of additivity of intermolecular forces, one has | ||
:<math>{\rm g}_1 (r_{12})= \int f (r_{13}) f(r_{23}) ~{\rm d} | :<math>{\rm g}_1 (r_{12})= \int f (r_{13}) f(r_{23}) ~{\rm d}{\mathbf r}_3</math> | ||
| Line 17: | Line 20: | ||
+ 2\psi (r_{12}) + \frac{1}{2} \chi (r_{12})</math> | + 2\psi (r_{12}) + \frac{1}{2} \chi (r_{12})</math> | ||
where <math>r_{ik}</math> is the distance <math>| | where <math>r_{ik}</math> is the distance <math>|{\mathbf r}_i -{\mathbf r}_k|</math>, where <math>f(r)</math> | ||
is the [[Mayer f-function]] | is the [[Mayer f-function]] | ||
| Line 24: | Line 27: | ||
and | and | ||
:<math>\varphi (r_{12}) = \int f (r_{13}) f (r_{24}) f (r_{34}) ~ {\rm d} | :<math>\varphi (r_{12}) = \int f (r_{13}) f (r_{24}) f (r_{34}) ~ {\rm d}{\mathbf r}_3 {\rm d}{\mathbf r}_4</math> | ||
:<math>\psi (r_{12}) = \int f (r_{13}) f (r_{23}) f (r_{24}) f (r_{34}) ~ {\rm d} | :<math>\psi (r_{12}) = \int f (r_{13}) f (r_{23}) f (r_{24}) f (r_{34}) ~ {\rm d}{\mathbf r}_3 {\rm d}{\mathbf r}_4</math> | ||
:<math>\chi (r_{12}) = \int f (r_{13}) f (r_{23}) f (r_{14}) f (r_{24}) f (r_{34}) ~ {\rm d} | :<math>\chi (r_{12}) = \int f (r_{13}) f (r_{23}) f (r_{14}) f (r_{24}) f (r_{34}) ~ {\rm d}{\mathbf r}_3 {\rm d}{\mathbf r}_4</math> | ||
==See also== | |||
*[[Pair distribution function]] | |||
*[[Total correlation function]] | |||
==References== | ==References== | ||
<references/> | |||
;Related reading | |||
*[http://dx.doi.org/10.1063/1.1723737 John G. Kirkwood and Elizabeth Monroe Boggs "The Radial Distribution Function in Liquids", Journal of Chemical Physics '''10''' pp. 394-402 (1942)] | |||
*[http://dx.doi.org/10.1063/1.1703948 J. L. Lebowitz and J. K. Percus "Asymptotic Behavior of the Radial Distribution Function", Journal of Mathematical Physics '''4''' pp. 248-254 (1963)] | |||
*[http://dx.doi.org/10.1063/1.1725652 B. Widom "On the Radial Distribution Function in Fluids", Journal of Chemical Physics '''41''' pp. 74-77 (1964)] | |||
*[http://dx.doi.org/10.1143/JPSJ.12.326 Kazuo Hiroike "Radial Distribution Function of Fluids I", Journal of the Physical Society of Japan '''12''' pp. 326-334 (1957)] | |||
*[http://dx.doi.org/10.1143/JPSJ.12.864 Kazuo Hiroike "Radial Distribution Function of Fluids II", Journal of the Physical Society of Japan '''12''' pp. pp. 864-873 (1957)] | |||
*[http://dx.doi.org/10.1080/00268970701678907 J. G. Malherbe and W. Krauth "Selective-pivot sampling of radial distribution functions in asymmetric liquid mixtures", Molecular Physics '''105''' pp. 2393-2398 (2007)] | |||
*[http://doi.org/10.1063/1.4973804 Sergey V. Sukhomlinov, Martin H. Müser "Determination of accurate, mean bond lengths from radial distribution functions", Journal of Chemical Physics '''146''' 024506 (2017)] | |||
[[category: statistical mechanics]] | [[category: statistical mechanics]] | ||
Latest revision as of 09:18, 8 October 2019
The radial distribution function is a special case of the pair distribution function for an isotropic system. A Fourier transform of the radial distribution function results in the structure factor, which is experimentally measurable. The following plot is of a typical radial distribution function for the monatomic Lennard-Jones liquid.
Density Expansion of the radial distribution function[edit]
The radial distribution function of a compressed gas may be expanded in powers of the density [1]
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left. {\rm g}(r) \right. = e^{-\beta \Phi(r)} (1 + \rho {\rm g}_1 (r) + \rho^2 {\rm g}_2 (r) + ...)}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho} is the number of molecules per unit volume and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi(r)} is the intermolecular pair potential. The function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\rm g}(r)} is normalized to the value 1 for large distances. As is known, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\rm g}_1 (r)} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\rm g}_2 (r)} , ... can be expressed by cluster integrals in which the position of of two particles is kept fixed. In classical mechanics, and on the assumption of additivity of intermolecular forces, one has
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\rm g}_1 (r_{12})= \int f (r_{13}) f(r_{23}) ~{\rm d}{\mathbf r}_3}
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\rm g}_2 (r_{12})= \frac{1}{2}({\rm g}_1 (r_{12}))^2 + \varphi (r_{12}) + 2\psi (r_{12}) + \frac{1}{2} \chi (r_{12})}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r_{ik}} is the distance Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |{\mathbf r}_i -{\mathbf r}_k|} , where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(r)} is the Mayer f-function
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left. f(r) \right. = e^{-\beta \Phi(r)} -1}
and
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi (r_{12}) = \int f (r_{13}) f (r_{23}) f (r_{24}) f (r_{34}) ~ {\rm d}{\mathbf r}_3 {\rm d}{\mathbf r}_4}
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \chi (r_{12}) = \int f (r_{13}) f (r_{23}) f (r_{14}) f (r_{24}) f (r_{34}) ~ {\rm d}{\mathbf r}_3 {\rm d}{\mathbf r}_4}
See also[edit]
References[edit]
- Related reading
- John G. Kirkwood and Elizabeth Monroe Boggs "The Radial Distribution Function in Liquids", Journal of Chemical Physics 10 pp. 394-402 (1942)
- J. L. Lebowitz and J. K. Percus "Asymptotic Behavior of the Radial Distribution Function", Journal of Mathematical Physics 4 pp. 248-254 (1963)
- B. Widom "On the Radial Distribution Function in Fluids", Journal of Chemical Physics 41 pp. 74-77 (1964)
- Kazuo Hiroike "Radial Distribution Function of Fluids I", Journal of the Physical Society of Japan 12 pp. 326-334 (1957)
- Kazuo Hiroike "Radial Distribution Function of Fluids II", Journal of the Physical Society of Japan 12 pp. pp. 864-873 (1957)
- J. G. Malherbe and W. Krauth "Selective-pivot sampling of radial distribution functions in asymmetric liquid mixtures", Molecular Physics 105 pp. 2393-2398 (2007)
- Sergey V. Sukhomlinov, Martin H. Müser "Determination of accurate, mean bond lengths from radial distribution functions", Journal of Chemical Physics 146 024506 (2017)
